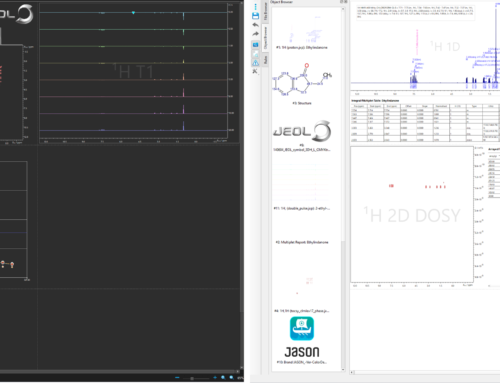
The next version of JASON, 3.0, is due to be released very soon. One of the most significant new features in this release will be support for 3D data, such as those routinely collected for biomolecular NMR applications. With this in mind, I thought I’d use this post to give a brief overview of all available processing functions implemented in JASON 3.0. More detailed descriptions of the individual functions will be covered in future blog posts. Figure 1 presents an example using a 3D HNCA spectrum kindly donated by our colleagues from JEOL USA for the development and testing of JASON. The currently applied processing is shown on the left side in the “Processing” panel. The 3D list is easy to spot from the direct dimension declared as F3 while the two additional, indirect dimensions are F2 and F1. The “Edit processing” dialog is floating above the selected F3(1H)-F1(13C) 2D plane of the 3D spectrum on Figure 1. The list of all available processing functions is shown on the left side under the label “Available”. We simply use the left mouse button to drag and drop elements to our “Selected” list. The order of the available processing functions follows their typical order of use. For example, Apodization is above Fourier Transform and Baseline Correction is below it, reflecting the order in which we typically want to apply them.

Figure 1 Example 3D HNCA processing list in JASON with the “Edit processing” dialog showing all available processing functions (up to JASON 3.0) on the left side.
Inverse Fourier Transform can be applied to a spectrum to generate time-domain data.
Indirect FT mode provides the relevant transformations for States, TPPI and echo/antiecho data. It is used right after the start of a new, indirect dimension.
Phase FID is a function to apply a zero-order phase correction value in the time domain. It is used by automatic processing of Varian /Agilent files when reproduction of original processing requires, i.e. the corresponding parameter is active.
Shrink provides the left/right shift and dropping of data points to reduce the effective points for the transformations after it. It can reproduce multiple features of data processing. By default, we mean it to manipulate FID data and automatic processing imports the relevant parameters Vendor agnostically. Interesting, it is not limited to operate on time-domain data. We will discuss its specialized use cases in a later blog post.
Flatten is used for processing interferogram pure shift NMR data. It effectively flattens one of the indirect dimensions into the direct dimension, and therefore reduces the data dimensionality. Automatic processing takes care of setting up its parameters based on identification of experiments (i.e. when the watermark on the NMR plot works).
CSSF Processing is a dedicated function to provide advanced handling of CSSF data. It is not Vendor specific but as of now only the JEOL/Delta standard library contains relevant pulse sequence implementation. Other data formats are usually pre-processed by spectrometer when collected and therefore unable to take advantage of the improved data processing implemented in this function.
Solvent Filter can be used to remove a selected region from the spectrum by a simple digital filtering of the FID. It can be used multiple times in the same processing list if multiple solvent signals need to be filtered out. [Please bear in mind this is not a replacement for solvent suppression by advanced pulse sequence methods.] We will discuss some use cases of this function and the specifics of the JASON implementation in more detail in a future blog post.
NUS stands for non-uniform sampling and provides the reconstruction of a fully sampled FID from any non-uniformly sampled one. It is currently implemented for the indirect dimension of 2D experiments, but can also be used in the direct dimension for some rare experiments. The processing itself supports any dimensions, but the data import in JASON is the currently limiting factor and will be solved soon.
Linear prediction is very useful to improve resolution in the indirect dimension of truncated 2D or 3D data or 1D pure shift experiments. It also supports backward prediction option. There is ongoing development to split this function into two different one for clarity, splitting the functionality of backward and forward LP. When processing list contains both backward and forward LP (typically benchtop Oxford Instruments 2D data), then it is currently possible but not easy to navigate with a single LP function used twice.
Apodization is implemented in a novel, user-friendly way. In basic mode, we can simply drag a slider to find the best compromise between improving sensitivity or resolution. In advanced mode, we can set all the parameters exactly or use automatic options driven by a smart algorithm that takes into account both acquisition parameters and estimated average decay rate of the actual FID data.
Zero filling is used to append zero values to the data to increase digital resolution by a factor of two and provide smoothing beyond that when desired. It has been recently upgraded with options to round to the next power of 2, and to specify zero filling either as a multipler or extend data size up to an exact number.
Group delay correction and Restore group delay functions are typically not used directly but they are called by other functions internally when needed. They convert between digitally filtered data and its analogue form. The details of their implementation is not disclosed at this stage, and plays a crucial role in enabling Solvent Filter and backward-LP to work correctly with typical JEOL and Bruker 1D spectra in JASON.
Fourier Transform provides the essential transformation of FID to spectrum. It supports up to 3D data since JASON 3.0.
Chemical shift scaling enables correct processing of CRAMPS type solid-state and any other scaled experiments. It was recently upgraded to enable its use in any dimensions.
Tilt/Shear provides the 45 degree rotation needed for most homonuclear 2D-J spectra, and the similar transformations for solid state MQ MAS experiments.
Phase provides zero- and first order phase corrections and a variety of automatic and magnitude mode options.
Savitzky-Golay Smoothing and 2D Savitzky-Golay Filter is typically not used in processing lists. They are called upon by automatic 1D and 2D peak picking methods. Adding them to a processing list can enable visualization of the internal steps of our peak picking, and could be useful to assist in setting the customizable parameters of automatic peak picking in JASON.
Reverse simply flips the data, typically the spectrum. It is implemented both as an FT option and as a separate processing function to enable exact reproduction of all kinds of processing used with different Vendor data formats.
Peak Referencing can be used to search for the tallest peak in a specific region and reference the spectrum to a user-defined value. It can be confusing with some other functions when input parameters depend on reference, e.g. Solvent Filter region definition. It is recommended for batch processing of large number of data files, in particular with the
Re-sample function.
Baseline Correction provides a variety of different methods to flatten the baseline of the spectrum. It currently supports 1D, pseudo2D and 2D data; its full 3D support is under development in JASON 3.1.
Drift Correction is basically the same as zero-order baseline correction when used after FT, in the frequency domain. It is preferred for 1D and pseudo2D data processing while baseline correction is preferred with nD(n>=2) spectra due to the typical number of points being smaller in multidimensional data. The DC has a slightly different meaning when used in the time domain, before FT. In this case, it provides the legacy procedure to correct for unbalanced real and imaginary channels. This can be needed with very old data for example Varian Inova.
Symmetrization can be used on both 2DJ and homonuclear 2D spectra. It is not yet implemented for higher dimensions.
t1 noise suppression is an efficient method to reduce the vertical stripes often seen in 2D spectra. This should be used carefully, in many cases the results are mainly cosmetic and will not reveal hidden peaks from very poor quality data.
Sum traces reduces the dimensionality of the data by calculating the sum of user-defined regions either from rows of columns of a 2D plot.
External Command is a very powerful tool in JASON. It allows JASON to run any executable by your OS to manipulate the data points in the processing list at the point where it is placed. We provide some examples to use this by calling Python and Matlab scripts. Any specialized processing can be implemented in this way rapidly on the user side. Interestingly, we can also implement analysis methods using integrals or peaks, which belong to the spectrum. There is ongoing development to disentangle analysis methods from the processing in this framework. More details will be subject to further blog posts.
DOSY performs the relevant fitting on pseudo2D data and provides the Diffusion-Ordered Spectroscopy plot from its result. It can use user-defined integral regions or automatic peak picking or fit each data point independently. In the future, similar functions will be introduced for the typical relaxation data. In the meantime, charts can be manually created from integral tables and user-defined equations can be used for fitting the series of data using any arrayed experiment as the source file.
Re-sample can be used to standardize spectral data. When the spectrum width or spectrometer frequency is different, the digital form of the spectrum contains points which do not lie on the exactly same grid as in other spectra. With sufficiently high digital resolution this is very small, but it can be useful in some analyses to ensure data points are on the identical grid by using linear interpolation. This can be used in any dimensions in frequency domain.
<-Next dimension-> just increments the dimension and in the processing panel it triggers the bold text notices like “F1 (indirect) dimension:” in 3D processing. These text messages do not appear in 1D processing lists, and numbering of the dimensions follows the conventional method of starting the counter at the last indirect dimension of the data